◆ 伝達関数は、制御要素の動特性を、定量的に表現します。しかし、式の形ですから直感的ではありません。制御応答を、図の形で表わす方が、直感性に優れています。
最も直感性が高いのが「ステップ応答 」です。ステップ応答は、制御要素にステップ状の入力を加えたときの出力です (図 3-1-2 はステップ応答です)。
ステップ応答は、時間領域の応答ですが、伝達関数の形で求めることができます。ステップ波形のラプラス変換は 1 / s です。したがって、制御要素の伝達関数 F(s) のステップ応答出力 Y(s) は、
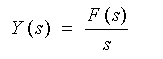・・・ (3-1-4)
となります。これを計算して、時間領域のステップ応答波形を求めることができます。
◆ PSPICE では、ステップ応答はトランジェント解析によって求まります。そして、トランジェント解析では、ラプラス変換を使用できます。
PSPICE では、伝達関数を使用できます(2.2.3.(2-A))。伝達関数は、ラプラス変換です。すなわち、制御要素の伝達関数を求めておけば、PSPICE でステップ応答を求めることができます。
◆ ステップ応答は直感性は、極めて高いのですが、制御要素の細かな特性を、表現することができません。直感性では、ステップ応答に劣りますが、詳細な特性を表わす点で優れているのが、「周波数応答 」です。
一般には「周波数特性 」と呼ばれていますが、制御の分野では周波数応答と呼んでいます。
周波数応答では、制御要素の入力に正弦波形を加えます (図 3-1-12)。
◆ 正弦波形を入力しはじめた直後には、過渡的な応答がありますが、やがて定常状態になり、出力も正弦波形 になります(図 3-1-13)。
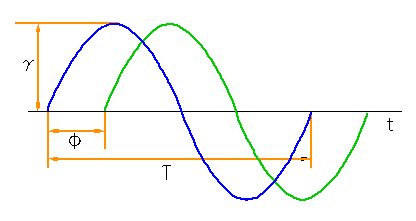
◆ この定常状態になった後の正弦波形の、入力と出力を比較すると、入力と出力との周波数は等しく、入出力間の振幅と位相は異なります。
入力正弦波形の周波数を変化させて、入力周波数に対する、入出力の振幅比および入出力の位相差の関係を求めたものを、周波数応答といいます。
そして、入力正弦波形の周波数 (対数) を横軸にとって、縦軸に振幅比(ゲイン) (dB) と位相差 (°) をプロットした図を、ボード線図 と呼んでいます。
PSPICE では、周波数応答を AC 解析によって求めることができます。PSPICE の AC 解析で求めた図(たとえば図 2-1-13)は、ボード線図です。AC 解析も、伝達関数を使用することができますから、PSPICE 上で、伝達関数から、ボード線図を求めることができます。
また、計算上も、周波数応答は、次に示すように、伝達関数から求めることが、非常に容易です。このことが、周波数応答を、より一層便利なものにしています。周波数応答は、フィードバック制御の解析、設計に広く使用されています。
◆ 周波数応答も、ステップ応答と同様に、正弦波形のラプラス変換を入力することによって、伝達関数から求めることも、できます。しかし、周波数応答を伝達関数から求めるのは、もっと簡単な、やり方があります。
周波数応答は、数学的には時間関数 f(t) にフーリエ変換という、変換を行ったものです。フーリエ変換 は、
・・・ (3-1-5)
です。ここで j は虚数 (-1 の平方根) です。
[注] 数学では、虚数を i で表します。しかし電気の分野では、i は、電流を表す記号として広く使われています。電流と混同しないために j を使用します。制御の分野でも、同様に j を使用します。
◆ ラプラス変換は、式 3-1-1 に示したように、時間領域の関数 f(t) に exp(-st) をかけて積分したものです。ここで
exp( ) は指数関数を表わします。
フーリエ変換は f(t) に exp(-jωt) をかけて積分します。すなわち、ラプラス変換で s→ jωと置き換えればフーリエ変換になります。
ラプラス変換のラプラス変換子 s は、実は複素数です。複素数 とは、二つの数を組み合わせたものです。そのとき、複素数では、一方を実数で、他方を虚数で表現します。実数部を x、虚数部を y とすれば、複素数は x + jy で表わされます。
複素数は 2 つの数の組ですから、平面で表現することができます。平面を x-y 座標で表わせば、複素数 x + jy は、x 軸が x、y 軸が y の、点で表わすことができます (図 3-1-14)。
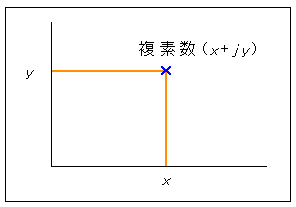
◆ 虚数 jy は、複素数 x + jy において、その実数部 x をゼロにした特殊形に過ぎません。
すなわち、フーリエ変換をさらに拡張し、一般化したものがラプラス変換だということです。
◆ フーリエ変換の exp(-jωt) は、外見は指数関数ですが、実は三角関数です。
exp(-jωt) = cos(ωt) - j sin(ωt)
の関係があります。
正弦関数 の振幅を γ、角速度を ω (周波数 f に対して、角速度ω = 2πf)、位相を φ とすれば、正弦関数は、時間領域では、
γ sin(ωt + φ)
です。
したがって、フーリエ変換は、
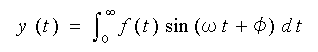・・・ (3-1-6)
を実行することと同じ意味を持っています。
周波数応答は、物理的な制御要素に、実在の正弦波形を入力して、その出力を求めたものです。式 3-1-6 は、数学的に、式の上で周波数応答を実行していると、考えることができます。
◆ 以上から、伝達関数のラプラス変換子 s を jω に置き換えることによって、周波数応答が求まることが分かりました。この伝達関数において s → jω と置き換えたものを、周波数伝達関数 ともいいます。
伝達関数は、ラプラス変換領域ですから、大文字を使用します。周波数伝達関数も、F(jω)のように表します。また、周波数領域 という呼び方をします。
周波数応答は、通常、入出力の振幅比(ゲイン) (dB) と位相差 (°) で表現します。上記の置き換えを行ったままでは、複素数表示です。複素数表示の周波数応答を、振幅比(ゲイン) (dB)と位相差 (°) による表現に換算することが必要です。
◆ 正弦関数は、ベクトルの形で、表現することができます (図 3-1-15)。
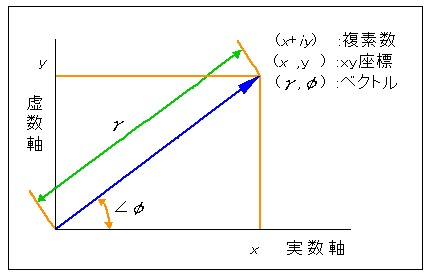
◆ ベクトル は大きさと方向を持つ量です。正弦関数の振幅 γ をベクトルの大きさで、位相 φ をベクトルの方向で表わします。方向を持つということは、ベクトルは、平面上に表わすことができる、ということです。
一方、複素数は、平面上の点として x-y 座標で表現することができます(図3-1-14)。すなわち、複素数はベクトルを表わすことができます。
[注] フーリエ変換の定義式は、純虚数 jω です。しかし、フーリエ変換された結果は、複素数です。すなわち、フーリエ変換された結果は、正弦関数を、ベクトルで表わしています。
◆ 図 3-1-15 から、式 3-1-7 の関係があることが分かります。ただし角度の単位は[rad]です。
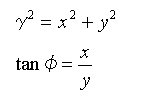・・・・ (3-1-7)
周波数応答は、通常、振幅比 (ゲイン) を対数 (dB) で表示し、位相差を度 (°) で表わします。したがって、複素数表示から、
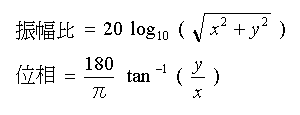・・・・ (3-1-8)
のように換算します。
◆ インピーダンス は、直流における抵抗 R の概念を交流に拡張したものです。直流においては、電圧を v、電流を i とすれば、
v = R i
です。
交流は正弦波形であり、かつ位相を考える必要があります。したがって、ベクトルで表わすことができます。すなわち、交流では電圧も電流もベクトルで表わされます。電流と電圧との関係を表わすインピーダンス Z もベクトルになります。
V = Z I
ベクトルですから、時間関数をフーリエ変換して表わすことができます。電圧と電流の関係、すなわちインピーダンスは、周波数伝達関数です。したがって、伝達関数で、s→jω とすることによって、インピーダンスになります。
