

◆ 複数の交流信号が存在するときは、その相互関係、すなわち、互いの時間的な ずれ を考える必要があります。図 2.2-2 の交流を一般化して表すと、図 2.2-8 のようになります。図で Vm は、最大値です。交流では、通常は実効値を使用しますから、換算の必要があります。
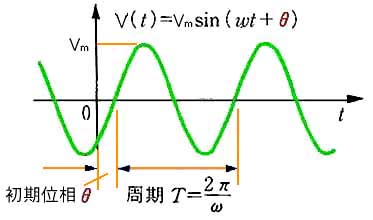
◆ ここで、sin の中身である、(ωt+θ) のことを、位相 といいます。また、時間 t = 0 のときの値、すなわち θ を初期位相 と呼んでいます。図の初期位相は、マイナスです。
複数の、周波数が等しい交流は、初期位相が異なると、互いに時間的な ずれ があります(図 2.2-9)。
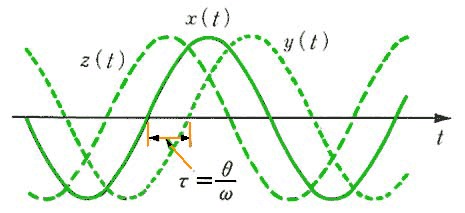
◆ x(t) = sin(ωt) を中心として、z(t) = sin(ωt+θ) は、時間的に先行し、y(t) = sin(ωt-θ) は、遅れています。互いの位相の差は、θ です。これを、位相差 といいます。
◆ 以上から、交流では、位相が重要な役割を持っていることが、想定されます。位相や、互いの位相差が、よく分かるような、交流の表現方法を、考えてみましょう。
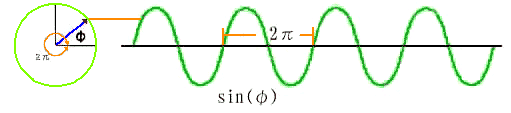
通常の交流は、正弦波です。正弦波 sin(ωt) は、2π (π は円周率 ≒ 3.14) ごとの繰り返しになります。したがって、ぐるぐる回る形で表現することができます(図 2.2-10)。図で、茶色の線が、一端を固定して、他端が回っている棒です。この棒の他端の高さが、sin(φ) になります。このことは、逆にいうと、回っている線が、sin(φ) を表現していると、考えることができます。位相を、動画で説明します。右記の「位相」をクリックしてください。戻るときは、ブラウザの「戻る」を使用してください。
◆ 交流を、このような、方向を持つ棒の形で表すことを、ベクトル表示 といい、この方向を持つ棒のことを、ベクトル といいます。ベクトルは、大きさだけでなく方向を持つ量です。これに対して、通常の量は、単に大きさを持つだけで、方向性はありません。この通常の、方向性を持たない量のことを、ベクトルに対して、スカラー といいます。
図 2.2-9 を、ベクトル表示で表すと、図 2.2-11 になります。位相差を保ったまま、回転している様子が良く分かります。
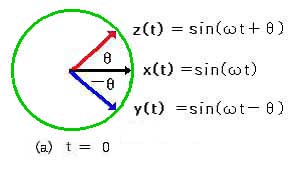
◆ 交流は、ベクトルで表すと、便利です。ここで、ベクトルの取り扱いについて、説明しておきましょう。
交流は、位相を考えると、大きさと向きの、2 つで表すことができます。したがって、すでに示したように、2 次元の空間、すなわち平面で表せます。平面は、グラフで、分かりやすく表すことができます。
ベクトルは、一般化すると、n 次元のベクトルで、n 次元の空間を表します。しかし、交流は 2 次元で表せますから、平面(2 次元)として、説明します。
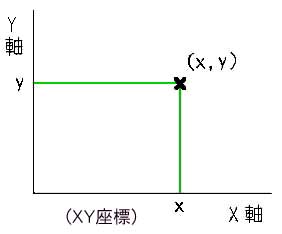
◆ 平面上の点は、2 つの数の組として表すことができます。2 つの数の組は、グラフの形で分かりやすく表示することができます。最も普通には、xy 座標 による表示ですが、極座標 も使われています(図 2.2-12)。
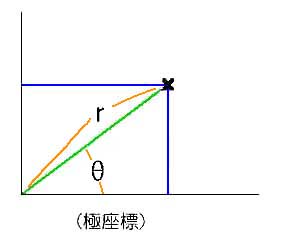
◆ 極座標と、ベクトル表示とを比べると、ほぼ同じものであることが分かります。したがって、ベクトル表示は、極座標で表すのが便利です。極座標は、必要に応じて、xy 座標と相互変換することができます。
xy 座標と、極座標との換算は、
x = r sin(θ)
y = r cos(θ)
です。
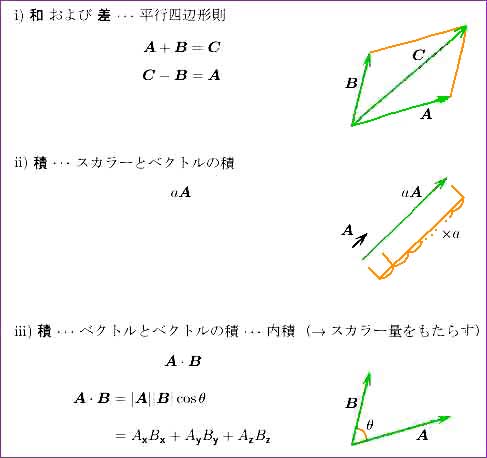
ベクトルの演算は、図で示す方が分かりやすいので、図 2.2-13 に示します。これも動画を示します(戻るときは、ブラウザの「戻る」を使用)。
図の他にもいろいろな表し方がありますが、次に示す、複素数の性質と重複しますから、そちらを見てください。
◆ 以上の座標系とは別に、複素数 (コラム 2.2-2)による表示法もあります。座標表示という点だけから見ると、基本的には、xy 座標や、極座標表示と、あまり変わりません。しかし、複素数による表示は、理論的には、ベクトル表示や、ベクトル表示をさらに発展させたものと、良く結びつけることができるので、優れた表示方式です。
複素数は、数学として深く理解する必要はありません。要は、平面を表すのには、2 つの変数が必要だということであり、複素数は、2 つの変数を表す表し方の 1 つだということです。すなわち、複素数は、平面の表し方の 1 つだということです。
◆ しかし、複素数について、一応簡単に説明しておきます。
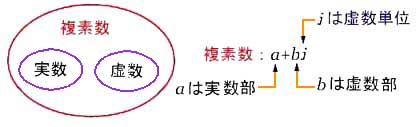
−1 の平方根、√-1 は、虚数 です。数学では、虚数を、i で表しますが、電気の分野では、i を電流の意味で使用します。電流と混同しないように、電気の分野では、虚数を j で表します。
虚数と実数とを組み合わせたものが複素数です([コラム 2.2-2] 参照)。
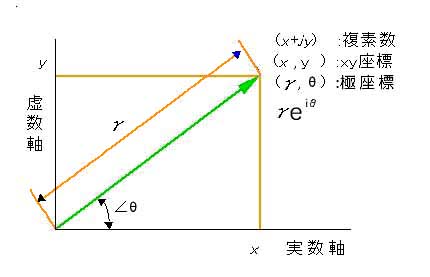
◆ 複素数で表した平面を、複素平面 といいます。複素平面による座標表示を、図 2.2-14に示します。図で、ejθ は、
ejθ = cos(θ) + j sin(θ) (オイラーの公式)
です。したがって、r ejθ は、ベクトル表示の 1 つの形式です。
★ 複素数は、実数 と虚数 との、2つの数の組み合わせで表される数です。しかし、複素数の言葉だけから考えると、二つの素数ということになります。そこで、ちょっと、素数について、調べて見ましょう。素数 は、1 を除く、自然数(ここで、自然数 は、1、2、3 、・ ・ ・)で、自分自身以外では、割り切れない数です。1000 までの素数は、下図の通りです。
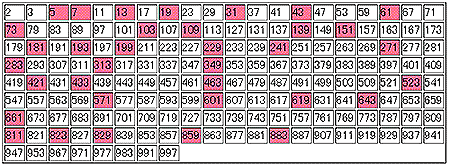
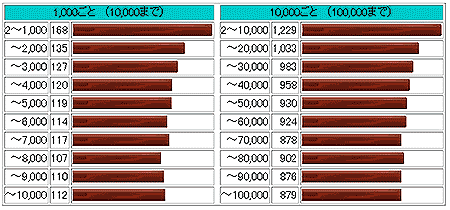
★ 素数は、合い隣る素数の差が、2 である数が、沢山あります。これを、双子素数 といいます。上図で、双子素数の大きい方の数を、桃色で示してあります。素数が、全体の自然数の中で、どのぐらいあるかを、下図に示します。
★ さて、複素数のお話に入ります。
私たちが使っている普通の数は、実数です。下記の図で、小数は、分数に含まれます。

★ 実数の重要な性質に、連続ということがあります。連続とは、値がつながっていて、切れ目が無いということです。
★ 最近は、世の中のものが、どんどんディジタル化される傾向にあります。しかし、私たちが住んでいるのは、アナログの世界です。電気も、電流、電圧など、全てアナログです。アナログは、連続であり、ディジタルは、非連続です。
もっとも、電流は、電子の流れであり、電子は、数を数えることができますから、原理的には、ディジタルです。
★ しかし、その数が、あまりにも多いので(1 クーロンの電荷は、電子の数が、約 1019 です)、実際に数で勘定することはできません。実用上は、電流もアナログです(数学と異なり、この辺のお話は、おおらかです)。
★ 虚数は、x2 = -1 の根です。x が実数のとき、x2 ≧ 0 ですから、x2 = -1 の根は、むなしい(本来あり得ない)数です。このことから、虚数と名付けられました。しかし、むなしい、どころか、虚数は、多いに役立っています。
★ 数学では、虚数を i で表しますが、電気の分野では、i は、電流の意味で使っています。それと混同しないように、「j」 を使用します。虚数にも大きさがあります。j は、大きさが 1 の虚数であり 虚数単位 といいます、任意の大きさの虚数は、a を任意の大きさの実数とすれば、「ja」で表します。
★ 虚数の基本的性質を、次に示します。
j2 = -1, j3 = -j, j4 = 1, j5 = -j ・ ・ ・ (1)
1/j = j4/j = j3 = -j, 1/j2 =-1, 1/j3 = j, 1/j4 = 1 ・ ・ ・ (2)
a>0 ならば、√-a = j√a, a>0,b<0 ならば、√ab = -√a√b
a>0,b<0 ならば、√b/a = √b/√a, √a/b = -√a/√b
★ 複素数とは、2 つの実数を、a および b とすれば、次のようになります。
★ 複素数の四則演算は、a,b,c,d が実数のとき、
(a + jb) + (c + jd) = (a + c) + j(b + d)
(a + jb) - (c + jd) = (a - c) + j(b - d)
(a + jb)(c + jd) = (ac - bd) + j(ad + bc)
(a + jb)/(c + jd) = (ac + bd)/(c2 + d2) + j(bc - ad)/(c2 + d2)
その他の複素数の基本的性質は、
a + jb = c + jd ならば、a = c, b = d、 a + jb = 0 ならば、a = b = 0
√(a2 + b2) を、a ± jb の絶対といい、|a ± b | で表します
2つの複素数、a + jb と a - jb とを、共役複素数と言います。共役複素数には、つぎの関係があります。
(a +jb) + (a - jb) = 2a, (a + jb)(a - jb) = a2 + b2
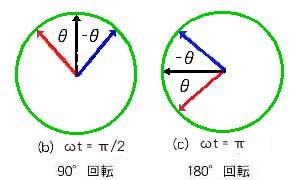
前記の虚数の性質 (1) は、複素数で考えると、j を掛けることは、反時方向に 90°回転させることを意味します。また (2) は、j で割ることは、時計方向に 90°回転させることを意味します。