◆ アナログ制御ではラプラス変換を使用して、伝達関数を導入しました。また周波数応答は伝達関数との結び付きがよく、これらを利用することによって、制御系の解析、設計を便利に行なうことができました。
またさらに、伝達関数を使用して、PSPICE によるシミュレーションを行うことができました。
デイジタル制御においても、アナログ制御と同様の表現や取り扱いができると便利です。
◆ ディジタル制御では、ラプラス変換の代わりに、Ｚ変換 という変換を行なうことによって、アナログ系のラプラス変換と、同様な取り扱いをすることができます。
◆ アナログ系においては、遅れのある制御要素は、積分で表わすことができました。遅れがあるということは、過去の値が現在に影響しているということです。このことが式の上では、積分になります。
ディジタル系においても、同様の理由によって、遅れのある制御要素は、過去のサンプル値を加算した形で、表わすことができます（図 4-1-16、式 4-1-10)。
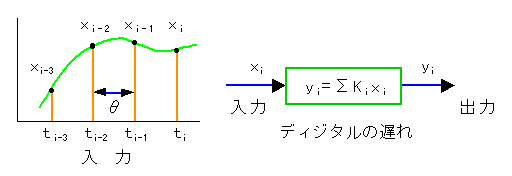
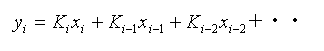・・・・ (4-1-10)
◆ ここで Ki は重みです。この重みを変えることによって、色々な特性の遅れを作ることができます。
◆ 図 4-1-16 で表わされる制御要素は。図 4-1-17のようにしても、全く同じ結果が得られます。
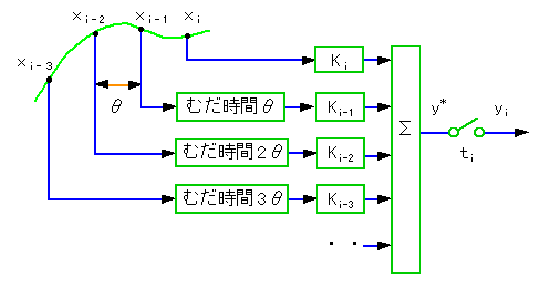
◆ 図で加算（Σ）までの演算はアナログです。そして加算された結果のアナログ値 y* を、時刻 ti でサンプリング(ディジタル化)します。
図で、サンプリングはスイッチの記号になっています。サンプリングの動作がスイッチ動作に似ているので、ブロック図の上では、サンプリングを、スイッチの記号で表わします。
既にサンプル値になっているデータを、もう一度同期してサンプリングしても、何も変化は起こりません。
この事実を利用して、そのデータがサンプル値であることを強調して示したいときに、実際にはその場所でサンプリングをしていなくても、ブロック図にサンプリングの記号を記入することがあります。
たとえば図 4-1-16のブロック図は、その出力のところで、実際にはサンプリングしていません。これを、図 4-1-18のように表わすことができます。
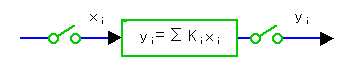
◆ 図 4-1-17の Σ までのところはアナログ系です。したがって、ここまでの部分は、伝達関数で表わすことができます。むだ時間θの伝達関数はexp(-θs)ですから(3.1.3.(4-4)式 3-1-18)、
・・・ (4-1-11)
となります。この式 4-1-11 は、アナログ系（非サンプリング）です。この出力を現時点 ti でサンプリングすればディジタル化され、式 4-1-10 のディジタル系（サンプリング系）と同じものになります。
◆ 式 4-1-11 の表現を簡単化するために、
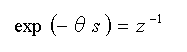・・・・ (4-1-12)
と置き換えると、たとえば
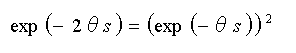・・・ (4-1-13)
ですから、
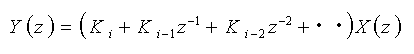・・・ (4-1-14)
となります。これは z の関数です。そして、ディジタル系をこの式 4-1-14 の形で表わすことを Z 変換 と呼びます。
◆ 以上述べたことから、Z 変換とは、サンプリング系が、時間領域で式 4-1-10 の形で表わされているときに、
・・・・ (4-1-15)
のように置き換える変換をいいます。式 4-1-12 から分かるように、Z 変換の z は、サンプリング周期を表わしています。
Z 変換は、ディジタル系(サンプリング系)で定義されたものです。したがって、サンプリング時点の値のみが、意味を持ちます。
アナログ系で、ラプラス変換領域の言葉を使うのと同様に、ディジタル系において、Z 変換領域 の言葉を使用します。
◆ ラプラス変換から伝達関数を導いたように、Z 変換から、ディジタル系の伝達関数を定義することができます。式 4-1-14 から、
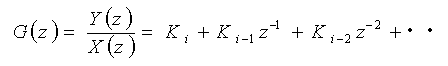・・・ (4-1-16)
が得られ、伝達関数 G(z) が導かれます。ディジタル系だけを取り扱う場合には、通常この G(z) のことを、単に伝達関数と呼んでいます。
しかし、アナログ系の伝達関数と区別して呼ぶ場合には、Z 変換から導いたディジタル系の伝達関数 G(z) をパルス伝達関数 と呼びます。
この講座では、アナログ系とディジタル系と両方を扱います。混同を避けるために、ディジタル系の伝達関数は、必ずパルス伝達関数と呼ぶことにします。アナログ系の伝達関数は、通常単に伝達関数と呼びます。
パルス伝達関数も、大文字で書いて、時間領域の関数と区別します。ただし伝達関数も大文字で表していますから(3.1.1(5-B))、X(z)、X(s) のように書かないと、相互を区別することはできません。
◆ Z 変換は、アナログのラプラス変換から導かれています。したがってパルス伝達関数は、(アナログの)伝達関数と同じ性質を持っています。たとえば、ブロック図の変換法則は、パルス伝達関数にも適用されます。
式 4-1-14 を見ると、無限の過去からの影響を受けるパルス伝達関数は、無限級数になります。
たとえば n 次遅れは、理論的には無限の過去からの影響を受けます。
しかし無限級数の形で表わされるパルス伝達関数は、一般に、簡単な有限の関数に変形することができます。
◆ 具体例として、ディジタル積分 の、パルス伝達関数を求めてみましょう。ディジタル時間領域の積分は、式 4-1-2 または、式 4-1-3 です。この式は簡単化して書いてありますが、無限級数です。したがって、式 4-1-2 の積分のときは、
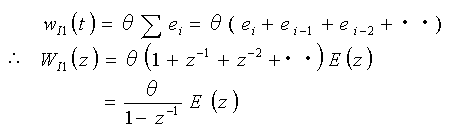・・・ (4-1-17)
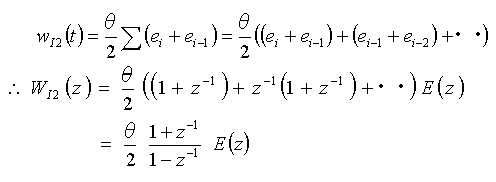・・・(4-1-18)
となります。
式 4-1-17、式 4-1-18 の最終変形は、
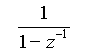・・・ (4-1-19)
の割り算（四則演算）を実行してみれば分かります。
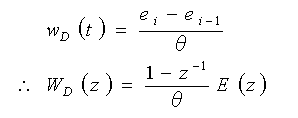・・・・ (4-1-20)
となります。
◆ 以上の結果、およびアナログ積分とアナログ微分の関係を総合して、表の形にまとめると、
◆ のようになりいます。
この表で、アナログの時間領域とラプラス変換領域相互、またはディジタルの時間領域とZ変換領域相互は、同じものを表わしており、その表現が異なるだけです。
しかし、アナログ系とディジタル系とは、単に表現の違いではなく、系自体を取り換えたときの対応を意味します。
[注] 表 4-1-4 は、たとえば、アナログ系の積分の出力をサンプリングしたときの対応を示すものではありません。たとえば、アナログ回路で構成された積分器と、マイコンのソフトウェアで演算するディジタル積分器との対応です。
