

★ 論理とは、議論の筋道、または、ものの考え方のことです。したがって、論理は、数学の世界のものだけではありません。私達が、日常使っている言葉にも適用されます。日本語は、非論理的な言語である、と言われています。しかし、日本語が、全く非論理的であったら、会話は、成り立ちません。ただ、英語などと比べると、その傾向はあります。
★ 英語の、AND、OR に対して、日本語の および、または の方が、意味があいまいです。英語には、AND/OR の言葉がありますが、日本語では、このような使い方は、ありません。日本語の、および には、英語の AND/OR の意味も含んでいるかです。
および と言ったとき、どちらの意味であるかは、前後の文章から、推定するしか、ありません。
★ しかし、英語も、数学ではなく、自然言語 (自然にできあがった言語)ですから、100 % 論理的では、ありません。これに対して、たとえば、コンピュータのプログラム言語は、人工言語 です。人工言語は、必要なら、コンピュータのプログラム言語 のように、100 % 論理的にすることが、できます。
★ 文学の世界は、論理的である必要はありません。美しければ良いわけです。
これに対して、数学の世界は、100 % 論理の世界です。技術の世界は、できるだけ論理的でありたいのですが、完全に論理的では、あり得ません。技術的な製品であっても、性能に大差が無ければ、デザインの良い方が、多く売れるでしょう。
| 美 | 論理 | |
| 文学 | 大いに必要 | 不要 |
| 一般の言語 | ある程度必要 | ある程度必要 |
| 技術文書 | ある程度必要 | 大いに必要 |
| 数学 | 不要 | 絶対に必要 |
★ しかし、美が不要であるはずの、数学の定理も、何故か、美しさがあります。たとえば、ピタゴラスの定理は、美しいと思います。
★ さて、論理学 とは、推論 の術であると、言われています。推論のやり方の定石を、知っておくと、論理の間違いを避けることが、できます。
★ 推論のやり方の定石を、例題によって、示すます。
[例題 1]
(A) 中村君は進級できない。(結論 )
(B) なぜなら、中村君が、要出席日数の 1/3 以上欠席したら、彼は、進級できない。(第 1 前提 )
(C) ところが、中村君は、要出席日数の、1/3 以上を欠席した。(第 2 前提 )
[例題 2]
(a) 中村君が、要出席日数の 1/3 以上欠席したら、彼は、進級できない。(第 1 前提)
(b) ところが、中村君は、要出席日数の、1/3 以上を欠席した。(第 2 前提)
(c) ゆえに、中村君は進級できない。(結論)
★ この 2 つの例題は、論理(内容)は全く同じことを言っています。そして、どちらも、「第 1 前提」、「第 2 前提」、「結論」という、3 つの骨組みになっています。
★ しかし、文章を読んだときの、語感が異なります。例題 1 は、結論が強調されています。これに対して、例題 2 は、平板な文章です。
この例では。言葉の順序が、文学的要素になっています。文章を、飾り立てることだけが、文学的要素なのでは、ありません。
★ ここで、もう 1 つ、推論の例題を考えます。幾何に関する例題です。
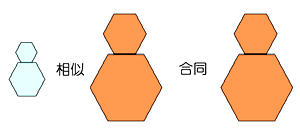
★ 順序は、すべて、「第 1 前提」、「第 2 前提」、「結論」という順序です。(1) は、三段論法 と呼ばれる形式です。(2)〜(4)には、否定文が入っています。否定文が入った論理は、注意しないと、間違います。
(1) 2 つの 3 角形が合同なら、それは相似である。
それらは合同である。
∴それらは相似である。(前件肯定 式)
(2) 2 つの 3 角形が合同なら、それは相似である。
それらは相似でない。
∴それらは合同でない。(後件否定 式)
(3) 2 つの 3 角形が合同なら、それらは相似である。
それらは相似である。
∴それらは合同である。(後件肯定 の誤り)
(4) 2 つの 3 角形が合同なら、それは相似である。
それらは合同でない。
∴それらは相似でない。(前件否定 の誤り)
★ ここで、前件、後件という言葉が、でできました。
「 xx ならば yy 」という文章を条件文 といいます。そして、この条件文の、xx のことを前件、yy のことを後件といいます。
★ 前記の誤りは、簡単な数学の問題ですから、すぐに、誤りであることが分かります。しかし、これが、一般の文章であると、上記の誤りを犯しても、気づかないことがあります。あるいは、間違って書かれているものを見逃して、しまいます。
なお、論理的に正しくても、その内容が、問題になります。
[例題 3]
風が吹けば桶屋が儲かる
今日は風が吹いている
∴今日は桶屋が儲かる
この例題では、第 1 前提は、そういうことも、あるかもしれない、という程度の、きわめて不確かな、前提です。不確かな前提からは、不確かな結論しか、導くことが、できません。
★ 不思議な国のアリス、および鏡の国のアリスという、童話があります。


★ この童話は、内容は、童話ですから、真実ではありません。しかし、論理的、数学的には、実に、計算し尽くされており、論理の間違いは、ありません。幾つかの大学で、論理学の授業に使ったという話があります。
それも、そのはずで、この童話の作者、ルイス・キャロルは、イギリスの、オックスフォード大学の、論理学と、数学の先生だった人です。
★ 論理的に正しいということと、内容が真実であるということとは、同じではありません。桶屋の例は、内容が、うそとまでは、ゆきませんが、きわめて、あやふやな内容です。
逆に、内容が真実であっても、論理の記述が間違っていると、その内容を、正しく伝えることが、できません。
★ この「お話」は、できるだけ、正しい内容を、できるだけ、分かり易く書くように、心掛けています。
正しい内容を、伝えるためには、論理的な記述が、必須です。
ただし、デバッグ(見直し)が、不充分なために、多分、このお話でも、論理の誤りを犯しているところがあると思います。
★ しかし、論理的に正しくても、それだけでは、分かりやすくは、なりません。
分かりやすくするための、手段として、分かりやすい文章、すなわち、文学的な要素も必要です。不思議な国のアリスが、童話として優れているのは、その文学性にあります。
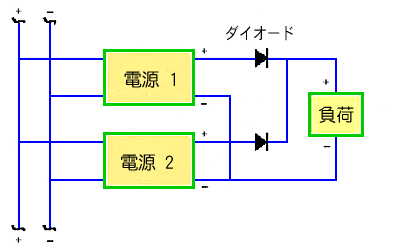
★ 分かりやすくするための手段の 1 つに、冗長性 があります。冗長 とは、重複する無駄のことです。この意味では、冗長は、不要な存在です。しかし、だから、冗長は、約に立たないということでは、ありません。冗長が役に立つ場合もあります。下図は、1 台で仕様を満足する機器を、2 台設置することによって、一方が故障しても、動作を継続することができるシステムです。この場合の冗長は、故障対策として、役立っています。図のダイオードは、故障時の自動切り替えスイッチです。
★ 私達は、生まれてから、いろいろな作業を、繰り返しによって、身に付けてきました。歩けるようになったのも、しゃべれるようになったのも、この繰り返し、すなわち冗長 のおかげです。学習には、冗長(繰り返し)が必要です。
★ この、お話でも、繰り返しによる、冗長を、活用しています。ただし、同じ言葉の繰り返しでは、読み易さに、つながりません。言葉の言い換えを利用しています。
★ 数は、10 進数と、2 進数の他にも、いろいろあります。私達の日常生活でも、10 進数や、2 進数以外の数を、ずいぶん、使用しています。
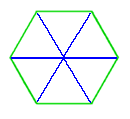
★ まず、時間があります。時間 は、1 日が、太陽の 1 回転(実は地球の 1 回転)することを、基準としています。したがって、角度から生まれたものです。角度 は、等分割の容易な角度を基準とすることが、自然の成り行きです。2、4、8 ・ ・ ・ も容易な分割数ですが、6 分割(60°)も、正 3 角形から、容易に作れます。そして、正 6 角形の作図も容易です。
★ 時間の、12 時間制 や、24 時間制 が生まれたのも、3、6、12・ ・ ・ の系列からです。角度の、360 進 も、時間の分割をさらに細分してできあがったものと、思います。
★ 12 という数は、6、4、3、2 と多くの数で割り切れます。これは、便利な性質です。この点、10 は、5 と 2 の 2 だけでしか割ることができません。
もし、人間が、6 本指であったなら、私達は、12 進数を使っていたのに、と思うと残念です。
★ 2 進数は、電子回路や、コンピュータでは、多く使用します。しかし、2 進数は、桁数が、やたらに多いために、読むのも書くのも面倒です。
そこで、2 進数を、私達が、読んだり、書いたりする、便宜上の産物として、16 進数 (ヘキサデシマル )が作られました。ここで、注意しなければ、ならないのは、16 進数は、あくまでも、人間が、読み書きする便宜のための、ものだということです。コンピュータや、電子回路の中で、実際に使われているのは、2 進数です。
|
|
★ 私達が使ってる数は、10 進数ですから、10 から、15 までの数字は、ありません。したがって、A から F までの、文字を借用しています。このため、本来の文字と、16 進数の数字とを混同する恐れがあります。この対策として、下記のような、表記法があります。
| (a) | (b) | (c) | (d) | (e) | |
| 2 進数 | 1001(2) | 1001b | 1001B | _ | _ |
| 10 進数 | 15(10) | 15d | 15D | _ | _ |
| 16 進数 | 10(16) | 10h | 10H | 0x10 | #10 |
★ (a)、(b)、(c)は、数字の後に添え字を付けて区別する方法です。
(c)の、16 進数で、数の後に、H を付ける方式の場合に、たとえば、「ABH」のように、最初の数字が、A〜F のときは、さらに、その前に数字の 0 を付け加えて、「0ABH」のように、書きます。数字の 0 を付けないで、「ABH」のように書くと、数字であることが分からないので、文字の記号「ABH」と読み誤る恐れがあるからです。
★ (d)は、C/C++/Java などの、プログラム言語で使われている方式です。
(e)は、WEB(ホームページ)用の言語 HTML で使われています。
★ 16 進数は、4 ビット単位での区切りになります。この 4 ビット単位の区切りになるということも、16 進数の特長です。4 ビットというのは、都合の良い区切りです。
10 進数は、人間にとって分かりやすいので、電子回路や、コンピュータの内部でも、10 進数を 2 進数に換算しないで、10 進数のままで、取り扱いたいことがあります。このようなときに、電子回路やコンピュータでは、BCD と呼ばれる数を、利用します。BCD は、4 ビットです。しかし、4 ビットをフルに使わないで、10 進数の 9 の次は、上の桁に桁上がりします。
|
|
★ BCD のように、2 進数を使用して、特定の意味を表したものを、コード (符号 )といいます。2 進数や、あるコードを、別のコードに変換することを、エンコード (符号化 )といい、エンコードするための装置が、エンコーダ です。この逆の操作が、デコード /デコーダ です。
★ 文字 (英文字、英数字、かな文字、漢字など)も、コンピュータなどの内部では、2 進数を使って、コードで表します。英数字 とは、英文字 (A、B、C ・・ 、a、b、c ・・)と、ローマ数字 (1、2、3 ・・)とを合わせたものです。
英文字コード は 7 ビット、かな文字コード は 8 ビット、漢字コード は 16 ビットで表します。これを総称して、文字コード といいます。漢字コードは別として、その他の文字コードは、8 ビットに収まります。コンピュータの中では、8 ビットを単位とすると、取り扱いが便利です。8 ビットを 1 単位として、これをバイト (BYTE )と呼んでいます。
なお、ここでは、文字コードの詳細には触れません。別の講座を参照してください。